대부분의 프로그래밍 언어에 내장된 정렬 함수들은 이 퀵 정렬 알고리즘과 병합 알고리즘을 기반으로 만들어졌다.
그 중 하나인 퀵 정렬 알고리즘에 대해 학습해보자.
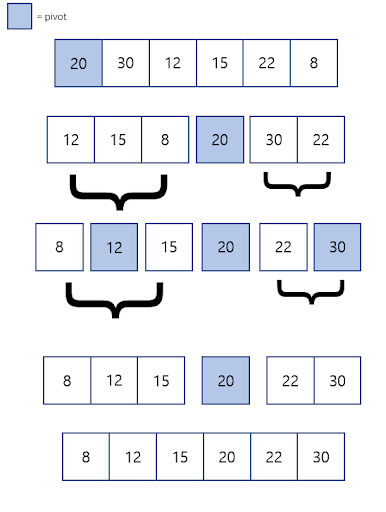
선택 정렬, 삽입 정렬이 데이터들을 순차적으로 비교하는 것과 다르게, 퀵 정렬 알고리즘에선 기준 데이터(Pivot)를 설정해 해당 값보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방식으로 정렬을 수행한다.
퀵 정렬 알고리즘이 작동하는 방식의 순서도는 다음과 같다.
1. 비교 기준이 될 pivot 인덱스를 설정한다. (기본적인 퀵 정렬 알고리즘에선 배열의 맨 처음 값을 pivot으로 설정한다.)
2. arr[pivot]부터 왼쪽부터 +1 씩 순차적으로 이동하며 arr[pivot]보다 큰 값을 찾는다.
3. 배열의 맨 뒤 값부터 순차적으로 -1 씩 감소하며 arr[pivot[보다 작은 값을 찾는다.
4. 만약 pivot부터 순차적으로 이동하며 찾은 큰 값의 인덱스가, 맨 뒤에서 -1씩 감소하며 찾은 작은 값의 인덱스보다 작다면, 큰 값과 작은 값의 값들을 스왑한다.
5. 만약 큰 값의 인덱스가 작은 값의 인덱스보다 커지면 (엇갈리게 되면), pivot값과 작은 값을 스왑한다.
이 과정을 거치게 되면 pivot값을 기준으로 왼쪽 데이터들은 arr[pivot]보다 작은 값들이, 오른쪽 데이터들은 arr[pivot]보다 큰 값들이 위치하게 된다.
즉, pivot을 기준으로 데이터가 분할된 것이다. 이렇게 분할된 데이터들에 대하여 계속 퀵 정렬을 반복해준다.
이러면 퀵 정렬 -> 데이터 분할 -> 퀵 정렬 -> 데이터 분할 -> 퀵 정렬 -> 데이터 분할 .... 의 과정을 거쳐 결국엔 데이터들이 정렬되게 된다.

위 과정은 재귀적 방식을 이용해 구현할 수 있다.
파이썬으로 구현한 퀵 정렬은 다음과 같다.
arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8] # 정렬되지 않은 array
def quickSorting(arr, start, end): # 정렬할 배열, 배열의 시작 인덱스, 마지막 인덱스
if start >= end: # 재귀함수를 끝내주기 위한 base case를 지정
return
pivot = start # 맨 왼쪽 값을 pivot
left = start + 1 # arr[pivot] 보다 큰 값을 저장할 left 인덱스
right = end # arr[pivot]보다 작은 값을 저장할 right 인덱스
while left <= right: # left와 right가 엇갈리지 않을 때까지
while left <= end and arr[left] <= arr[pivot]:
left += 1
while right > start and arr[right] >= arr[pivot]:
right -= 1
# while문을 빠져나오면 arr[left]와 arr[right]는 각각 arr[pivot]보다 큰 값, 작은 값을 갖는다.
if left > right: # left와 right가 엇갈린 경우
arr[right], arr[pivot] = arr[pivot], arr[right]
else: # 엇갈리지 않은 경우
arr[left], arr[right] = arr[right], arr[left]
# 배열을 pivot을 기준으로 두 개로 분할 후, 분할 된 배열 모두 퀵정렬 실행
quickSorting(arr, start, right - 1)
quickSorting(arr, right+1, end)
quickSorting(arr, 0, len(arr)-1)
print(arr)

퀵 정렬의 시간복잡도

퀵 정렬로 분할된 배열들을 각각 비교하면 총 배열의 길이 N만큼 연산을 수행하게 되고, 이걸 logN번(높이)만큼 반복하므로, 퀵 정렬의 시간복잡도는 NlongN이라고 할 수 있다.
하지만, 함수 실행 시 분할되는 배열의 균형이 한 쪽으로 치우처져 있다면 순환 호출의 깊이는 logN번이 아닌 N번이 되게 된다. 즉, 최악의 경우 (배열이 불균형할 경우) 퀵 정렬의 시간 복잡도는 O(N^2)이라고 할 수 있다.
앞서 설명했듯, 대부분의 프로그래밍 언어에서 제공하는 내장 정렬함수는 퀵 정렬과 병합 정렬을 혼합하여 사용하고 있다.
따라서, 배열이 불균형하다고 하더라도 그에 대한 대처를 다 해놓았기 때문에 NlogN의 시간복잡도를 보장하고 있다.
* 추가
리스트 컴프리헨션 방식을 통해 퀵 정렬 함수를 보다 깔끔하게 작성할 수 있다.
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[0]
rest = arr[1:] # 피벗 데이터를 제외한 리스트 값들
left = [x for x in rest if x <= pivot] # pivot보다 작거나 같은 값들을 따로 저장
right = [x for x in rest if x > pivot] # pivot보다 큰 값들을 따로 저장
# 나눠진 left, right를 재귀적으로 다시 정렬한 후 세 리스트를 더해준다.
return quick_sort(left) + [pivot] + quick_sort(right)'알고리즘 > 이론' 카테고리의 다른 글
| 투 포인터 알고리즘 (0) | 2021.02.01 |
|---|---|
| 소수판별 알고리즘 - 파이썬 (Python) (7) | 2021.01.31 |
| 선택 정렬, 삽입 정렬 알고리즘 with 파이썬 (Python) (0) | 2021.01.22 |
| 재귀함수 - 파이썬(Python) (0) | 2021.01.13 |
| 알고리즘과 알고리즘의 성능평가 (0) | 2021.01.07 |