투 포인터 알고리즘은 주로 수열의 연속된 값들의 합을 다룰 때 사용되는 알고리즘이다.
여기서 두 개의 포인터란 말 그대로 시작점과 끝 점을 포인터로 잡아 해당 포인터들이 움직이면서 동작을 수행해준다.
백문이불여일견. 이미지로 한 번 살펴보자
동작 방식
우리가 배열에서 연속된 값의 합이 5가 될 때의 경우를 찾고 싶다고 가정해보자.
물론 반복문을 두 번 중첩시켜 모든 배열의 값들에 대해 완전탐색을 진행할수도 있지만, 그러한 방식은 O(n^2) 만큼의 시간이 소요된다.
배열이 커지면 커질수록 연산시간은 기하급수적으로 증가할 것이다.
따라서 사용되는 방식이 이 글에 포스팅하는 투 포인터 방식이다.
앞서 설명한 것과 마찬가지로, 투 포인터 방식에선 start와 end라는 두 개의 포인터를 정의해준다.
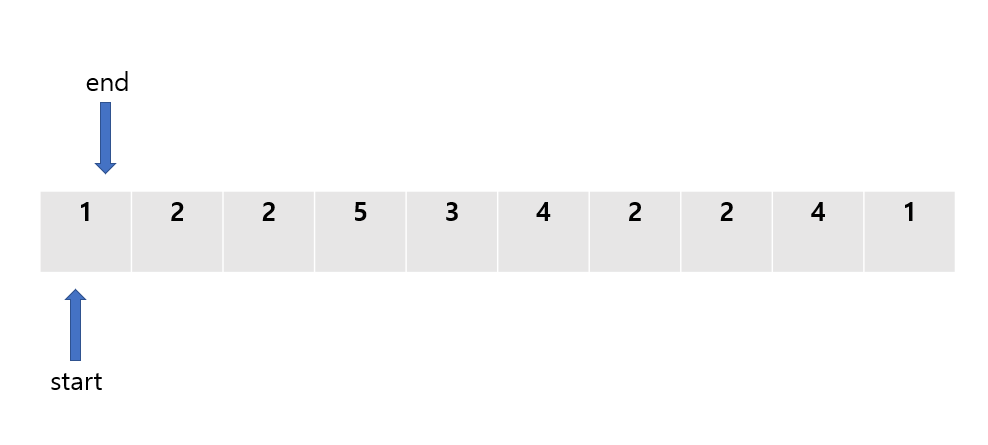
처음엔 두 포인터 모두 배열의 첫 번째 값을 갖게 해준다.
그리고 start ~ end에 있는 모든 값들의 합을 구한 후 그 값이 우리가 비교하고자 하는 값(5)과 일치하는지 확인해준다.
start ~ end의 모든 합은 1이므로, 우리가 찾고자하는 값보다 작다. 그렇다면, end 포인터를 1 증가시켜준다.

이제 다시 start ~ end의 모든 값들의 합을 구한 후 우리가 찾고자하는 값과 일치하는지 확인한다.
start ~ end의 모든 값들의 합은 3으로, 여전히 5보다 작은 상태이다. 다시 한 번 end 포인터를 1 증가시켜준다.
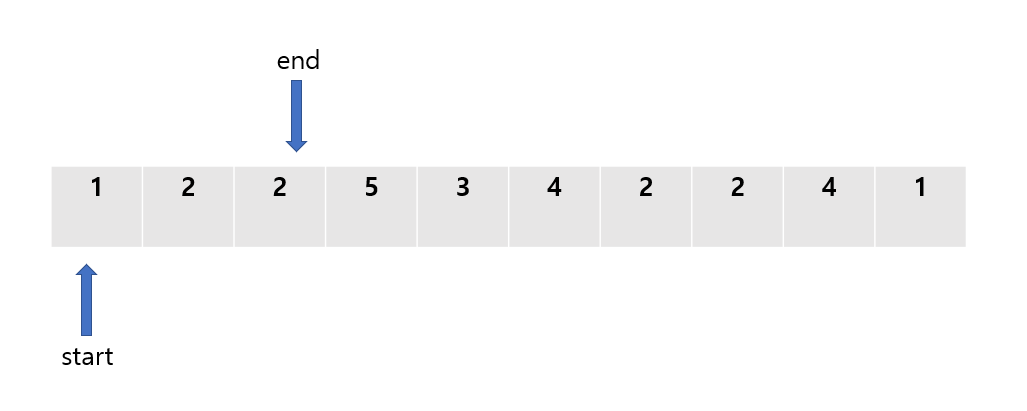
이제 end 포인터는 세 번째 값을 가르키게 되었으며, start ~ end의 모든 값의 합은 5가 되어 우리가 구하고자 하는 값과 일치하게 된다.
즉, 배열에서 연속된 값의 합이 5가 되는 경우의 수를 하나 찾은 것이다. 경우의 수를 하나 찾았다는 의미로 count라는 변수에 1을 추가해준다.
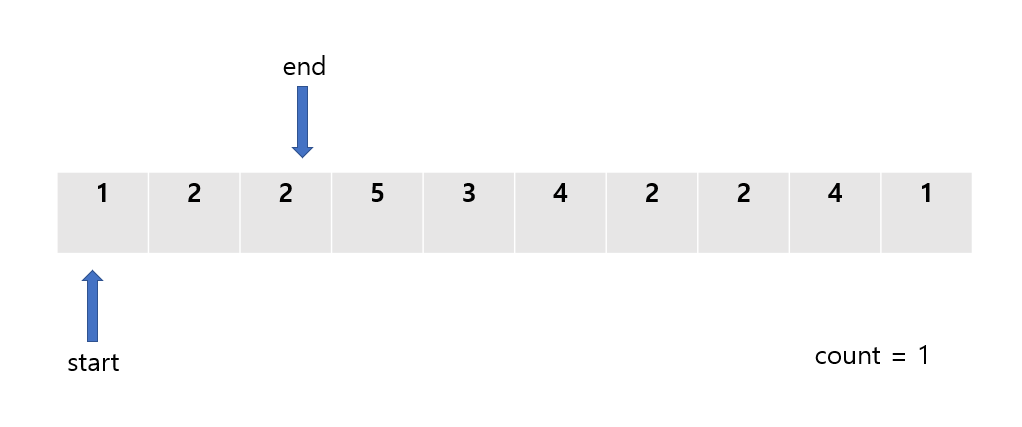
이제 다음 상황에서 end 포인터의 값을 늘리게 될 경우 start ~ end의 합은 무조건 5보다 커지는 상황이 발생하기 때문에, start 포인터 값을 1 증가시켜준다.

이제 다시 start ~ end의 값의 합은 4로, 우리가 구하고자 하는 값 5보다 더 작아지게 되었다.
그러면 이전의 방식과 동일하게 다시 end 포인터를 1 증가시켜 start ~ end 값의 합을 5와 비교시켜줄 수 있다.
위 과정을 end 포인터가 배열의 마지막 값에 도달할 때까지 반복해주면, 결국 우리가 찾고자 하는 값을 찾을 수 있을 것이다.
투 포인터 관련 문제
[백준] 2003번 수들의 합2 - seongonion.tistory.com/48
[백준] 2003번 수들의 합2 - 파이썬(Python)
문제 N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오. 입력 첫째 줄에.
seongonion.tistory.com
[백준] 1806번 부분합 - seongonion.tistory.com/49
[백준] 1806번 부분합 - 파이썬(Python)
시간 제한 메모리 제한 0.5 초 (하단 참고) 128 MB 문제 10,000 이하의 자연수로 이루어진 길이 N짜리 수열이 주어진다. 이 수열에서 연속된 수들의 부분합 중에 그 합이 S 이상이 되는 것 중, 가장 짧
seongonion.tistory.com
[백준] 1644번 소수의 연속합 - seongonion.tistory.com/50
[백준] 1644번 소수의 연속합 - 파이썬(Python)
시간 제한 메모리 제한 2 초 128 MB 문제 하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다. 3 : 3 (한 가지) 41 : 2+3+5+7+11+13 = 11+13+17 =
seongonion.tistory.com
'알고리즘 > 이론' 카테고리의 다른 글
| 계수(카운팅) 정렬 (Counting sort) with 파이썬(Python) (0) | 2022.02.10 |
|---|---|
| 거듭제곱 더 더 더 빠르게 with 파이썬(Python) (2) | 2021.09.07 |
| 소수판별 알고리즘 - 파이썬 (Python) (7) | 2021.01.31 |
| 퀵 정렬 알고리즘 with 파이썬 (Python) (0) | 2021.01.22 |
| 선택 정렬, 삽입 정렬 알고리즘 with 파이썬 (Python) (0) | 2021.01.22 |
투 포인터 알고리즘은 주로 수열의 연속된 값들의 합을 다룰 때 사용되는 알고리즘이다.
여기서 두 개의 포인터란 말 그대로 시작점과 끝 점을 포인터로 잡아 해당 포인터들이 움직이면서 동작을 수행해준다.
백문이불여일견. 이미지로 한 번 살펴보자
동작 방식
우리가 배열에서 연속된 값의 합이 5가 될 때의 경우를 찾고 싶다고 가정해보자.
물론 반복문을 두 번 중첩시켜 모든 배열의 값들에 대해 완전탐색을 진행할수도 있지만, 그러한 방식은 O(n^2) 만큼의 시간이 소요된다.
배열이 커지면 커질수록 연산시간은 기하급수적으로 증가할 것이다.
따라서 사용되는 방식이 이 글에 포스팅하는 투 포인터 방식이다.
앞서 설명한 것과 마찬가지로, 투 포인터 방식에선 start와 end라는 두 개의 포인터를 정의해준다.

처음엔 두 포인터 모두 배열의 첫 번째 값을 갖게 해준다.
그리고 start ~ end에 있는 모든 값들의 합을 구한 후 그 값이 우리가 비교하고자 하는 값(5)과 일치하는지 확인해준다.
start ~ end의 모든 합은 1이므로, 우리가 찾고자하는 값보다 작다. 그렇다면, end 포인터를 1 증가시켜준다.

이제 다시 start ~ end의 모든 값들의 합을 구한 후 우리가 찾고자하는 값과 일치하는지 확인한다.
start ~ end의 모든 값들의 합은 3으로, 여전히 5보다 작은 상태이다. 다시 한 번 end 포인터를 1 증가시켜준다.

이제 end 포인터는 세 번째 값을 가르키게 되었으며, start ~ end의 모든 값의 합은 5가 되어 우리가 구하고자 하는 값과 일치하게 된다.
즉, 배열에서 연속된 값의 합이 5가 되는 경우의 수를 하나 찾은 것이다. 경우의 수를 하나 찾았다는 의미로 count라는 변수에 1을 추가해준다.

이제 다음 상황에서 end 포인터의 값을 늘리게 될 경우 start ~ end의 합은 무조건 5보다 커지는 상황이 발생하기 때문에, start 포인터 값을 1 증가시켜준다.

이제 다시 start ~ end의 값의 합은 4로, 우리가 구하고자 하는 값 5보다 더 작아지게 되었다.
그러면 이전의 방식과 동일하게 다시 end 포인터를 1 증가시켜 start ~ end 값의 합을 5와 비교시켜줄 수 있다.
위 과정을 end 포인터가 배열의 마지막 값에 도달할 때까지 반복해주면, 결국 우리가 찾고자 하는 값을 찾을 수 있을 것이다.
투 포인터 관련 문제
[백준] 2003번 수들의 합2 - seongonion.tistory.com/48
[백준] 2003번 수들의 합2 - 파이썬(Python)
문제 N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오. 입력 첫째 줄에.
seongonion.tistory.com
[백준] 1806번 부분합 - seongonion.tistory.com/49
[백준] 1806번 부분합 - 파이썬(Python)
시간 제한 메모리 제한 0.5 초 (하단 참고) 128 MB 문제 10,000 이하의 자연수로 이루어진 길이 N짜리 수열이 주어진다. 이 수열에서 연속된 수들의 부분합 중에 그 합이 S 이상이 되는 것 중, 가장 짧
seongonion.tistory.com
[백준] 1644번 소수의 연속합 - seongonion.tistory.com/50
[백준] 1644번 소수의 연속합 - 파이썬(Python)
시간 제한 메모리 제한 2 초 128 MB 문제 하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다. 3 : 3 (한 가지) 41 : 2+3+5+7+11+13 = 11+13+17 =
seongonion.tistory.com
'알고리즘 > 이론' 카테고리의 다른 글
| 계수(카운팅) 정렬 (Counting sort) with 파이썬(Python) (0) | 2022.02.10 |
|---|---|
| 거듭제곱 더 더 더 빠르게 with 파이썬(Python) (2) | 2021.09.07 |
| 소수판별 알고리즘 - 파이썬 (Python) (7) | 2021.01.31 |
| 퀵 정렬 알고리즘 with 파이썬 (Python) (0) | 2021.01.22 |
| 선택 정렬, 삽입 정렬 알고리즘 with 파이썬 (Python) (0) | 2021.01.22 |
