트리 자료구는 이전에 살펴봤던 링크드 리스트, 해시테이블과는 다르게 데이터들을 계층적으로 저장하여 관리한다.
이말은 즉, 삽입된 데이터 간에 높낮이 혹은 서열이 있다는 뜻으로 이해할 수 있겠다.
링크드 리스트의 노드를 정의할 때 데이터 값과 다음 노드에 대한 레퍼런스를 next 라는 이름으로 저장한 것과 반대로,
트리의 경우 노드에 데이터값과 자신의 윗 노드, 아랫 노드에 대한 레퍼런스를 저장하고 이를 각각 부모노드, 자식노드라 칭한다.

root 노드
트리의 맨 시작점이 되는 노드이다. 링크드 리스트에서 head 노드를 따로 관리해줬던 것처럼 트리에서는 제일 윗 노드를 root라는 이름으로 따로 관리해준다.
형제노드(자매노드) Siblings
동일한 부모를 공유하는 다른 노드들을 말한다. 위 트리에선 F와 G가 서로 형제 관계에 있다고 볼 수 있다.
리프 노드 Leaf Node
나뭇잎이란 뜻으로, 말 그대로 자식을 갖지 않는 노드를 일컫는다.
부분 트리(서브 트리)
전체 트리 내부에서 이루고 있는 또 다른 트리를 일컫는다. 하위 트리 개념으로 생각할 수 있다.
레벨 (깊이)
트리의 특정 노드가 root 노드로부터 떨어진 정도를 이야기한다.
높이
레벨과 유사한 개념이지만, 각 노드의 특징이 아닌 트리 자체의 특징을 묘사하는 표현이라고 할 수 있다. 위의 트리는 3의 높이를 갖는 트리라고 할 수 있다. (높이는 0부터 시작)
이진 트리 (Binary Tree)
이진트리란, 각 노드가 최대 2개의 자식노드를 거느릴 수 있는 트리를 말한다. 이진 트리는 구현하기도 용이하고 쓰임새도 다양해 트리를 사용할 때는 일반적으로 이진 트리를 이용한다.
# 이진트리 노드 클래스 구현
class Node:
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
이진트리는 트리의 모양에 따라 다시 많은 종류로 나뉠 수 있다.
1) 정 이진트리 (Full Binary Tree)

정 이진트리는 모든 노드가 0 혹은 2개의 자식 노드를 갖는 트리를 말한다.
2) 포화 이진트리 (Perfect Binary Tree)
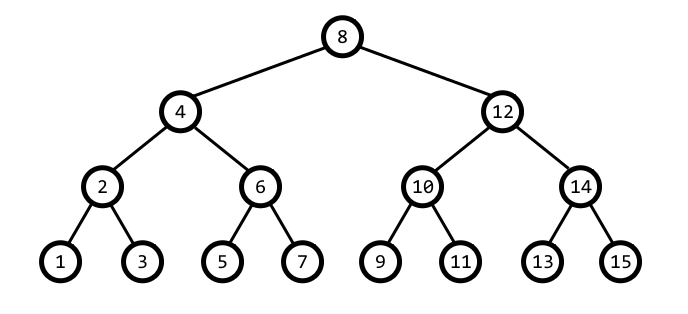
포화 이진트리는 트리의 모든 레벨의 노드들이 하나도 빠짐없이 가득 차 있는 트리를 일컫는다.
3) 완전 이진트리 (Complete Binary Tree)

완전 이진트리는, 트리의 마지막 레벨을 제외한 다른 레벨들에선 모든 노드들이 존재하며, 마지막 레벨의 노드는 왼쪽부터 빈틈 없이 채워진 트리를 말한다.
트리에서 가장 많이 사용되는 방식이 바로 이 완전 이진트리이다. 추후 다루게 될 우선순위 큐, 힙 등의 자료구조 또한 완전 이진트리의 조건을 갖춰야한다.
완전 이진트리의 특징 중 하나는 노드의 갯수와 트리의 높이와의 관계에서 찾아볼 수 있다.
완전 이진트리의 노드의 개수가 n개 일 때, 그 트리의 높이 h는 log(n)에 비례한다고 할 수 있다.
h = 0일 때 h레벨의 노드의 개수는 총 1개
h = 1일 때 h레벨의 노드의 개수는 총 2개
h = 2일 때 h레벨의 노드의 개수는 총 4개
h = 3일 때 h레벨의 노드의 개수는 총 8개
....
높이가 높아짐에 따라 각 노드 하나당 2개의 자식 노드가 생기므로 각 레벨마다 이전 레벨의 노드의 개수 * 2씩 개수가 증가하는 것을 확인할 수 있다.
이것을 알면 높이가 증가함에 따라 트리의 전체 노드 개수의 범위를 확인할 수 있다.
h의 높이를 가진 트리가 가질 수 있는 전체 노드 개수의 최댓값
h = 0 일 때 2^0 = 1개
h = 1 일 때 2^0 + 2^1 = 3개
h = 2 일 때 2^0 + 2^1 + 2^2 = 7개
h = 3 일 때 2^0 + 2^1 + 2^2 + 2^3 = 15개
....
h = h 일 때 2^0 + 2^1 + .... + 2^h 개
등비수열의 합의 공식을 적용하여 계산하면 전체 노드 개수의 최댓값은 2^h+1 -1개가 된다.
h의 높이를 가진 트리가 가질 수 있는 전체 노드 개수의 최솟값
h = 0 일 때 2^0 = 1개
h = 1 일 때 2^0 + 1 = 2개
h = 2 일 때 2^0 + 2^1 + 1 = 4개
h = 3 일 때 2^0 + 2^1 + 2^2 + 1 = 8개
....
h = h 일 때 2^0 + 2^1 + .... + 2^h-1 + 1 개
마찬가지로 등비수열 합의 공식을 적용하면 전체 노드 개수의 최솟값은 2^h개가 된다.
이걸 부등식으로 정리해보자.
높이가 h인 완전이진트리의 노드의 개수 n은
2^h <= n <= 2^h+1 -1 의 범위안에 있게 된다.
여기서, 높이는 무조건 정수이므로 위의 부등식은
2^h <= n < 2^h+1 로 다시 표현 가능하다.
이제 이 부등식의 모든 값들에 log를 씌워주면,
h <= log(n) < h+1 이 된다.
앞서 말했듯, h는 정수이므로 위 부등식은 "완전이진트리의 높이 h는 전체 노드의 개수 n보다 작은 정수 중 가장 큰 수"로 해석할 수 있다.
다시 말해, 만약 노드가 8개라면 log8 = 3이므로 완전이진트리의 높이는 3이되고,
노드가 11개라면 log8 (3) < log11 < log16(4) 를 만족하므로 여전히 높이가 3이라는 얘기가 된다.
여기서 재밌는 사실을 하나 더 알 수 있다. log n이 정수가 되기 위해선 당연히 2의 거듭제곱수가 되어야할 것이다. 즉, n은 적어도 자기보다 큰 수 중 2의 거듭제곱수보다 큰 숫자가 되어야 완전이진트리의 높이가 1 추가된다는 것이다.
즉, 노드의 개수가 11일 때는 11보다 큰 수 중 2의 거듭제곱 수, 즉 16보다 커지는 순간 트리의 높이가 1 추가된다.
1) 노드 개수 n이 주어질 때, 완전이진트리의 높이를 구하는 함수
# 노드 개수가 주어질 때 완전이진트리의 높이
def complete_binaryTree_height_with_node_number(n):
i = 0
while 2 ** i < n:
i += 1
return i - 1
print(complete_binaryTree_height_with_node_number(37))
2) 완전이진트리의 높이 h가 주어질 때, 해당 트리가 가질 수 있는 총 노드의 최대 개수를 구하는 함수 (재귀함수 이용)
# h 높이의 완전이진트리가 가질 수 있는 노드의 최대 개수
def complete_binaryTree_node_max_number_with_height(h): # 높이 h를 파라미터로
if h == 0: # base case
return 1
return (2 ** h) complete_binaryTree_node_max_number_with_height(h-1)
print(complete_binaryTree_node_max_number_with_height(3))
'그 외 공부 > 자료구조' 카테고리의 다른 글
| 힙(Heap) 자료구조 (0) | 2021.01.30 |
|---|---|
| 이진트리 및 완전이진트리 구현과 순회 (0) | 2021.01.30 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
| 해시테이블의 충돌방지 - Open Addressing (0) | 2021.01.15 |
트리 자료구는 이전에 살펴봤던 링크드 리스트, 해시테이블과는 다르게 데이터들을 계층적으로 저장하여 관리한다.
이말은 즉, 삽입된 데이터 간에 높낮이 혹은 서열이 있다는 뜻으로 이해할 수 있겠다.
링크드 리스트의 노드를 정의할 때 데이터 값과 다음 노드에 대한 레퍼런스를 next 라는 이름으로 저장한 것과 반대로,
트리의 경우 노드에 데이터값과 자신의 윗 노드, 아랫 노드에 대한 레퍼런스를 저장하고 이를 각각 부모노드, 자식노드라 칭한다.

root 노드
트리의 맨 시작점이 되는 노드이다. 링크드 리스트에서 head 노드를 따로 관리해줬던 것처럼 트리에서는 제일 윗 노드를 root라는 이름으로 따로 관리해준다.
형제노드(자매노드) Siblings
동일한 부모를 공유하는 다른 노드들을 말한다. 위 트리에선 F와 G가 서로 형제 관계에 있다고 볼 수 있다.
리프 노드 Leaf Node
나뭇잎이란 뜻으로, 말 그대로 자식을 갖지 않는 노드를 일컫는다.
부분 트리(서브 트리)
전체 트리 내부에서 이루고 있는 또 다른 트리를 일컫는다. 하위 트리 개념으로 생각할 수 있다.
레벨 (깊이)
트리의 특정 노드가 root 노드로부터 떨어진 정도를 이야기한다.
높이
레벨과 유사한 개념이지만, 각 노드의 특징이 아닌 트리 자체의 특징을 묘사하는 표현이라고 할 수 있다. 위의 트리는 3의 높이를 갖는 트리라고 할 수 있다. (높이는 0부터 시작)
이진 트리 (Binary Tree)
이진트리란, 각 노드가 최대 2개의 자식노드를 거느릴 수 있는 트리를 말한다. 이진 트리는 구현하기도 용이하고 쓰임새도 다양해 트리를 사용할 때는 일반적으로 이진 트리를 이용한다.
# 이진트리 노드 클래스 구현
class Node:
def __init__(self, data):
self.data = data
self.left_child = None
self.right_child = None
이진트리는 트리의 모양에 따라 다시 많은 종류로 나뉠 수 있다.
1) 정 이진트리 (Full Binary Tree)

정 이진트리는 모든 노드가 0 혹은 2개의 자식 노드를 갖는 트리를 말한다.
2) 포화 이진트리 (Perfect Binary Tree)

포화 이진트리는 트리의 모든 레벨의 노드들이 하나도 빠짐없이 가득 차 있는 트리를 일컫는다.
3) 완전 이진트리 (Complete Binary Tree)

완전 이진트리는, 트리의 마지막 레벨을 제외한 다른 레벨들에선 모든 노드들이 존재하며, 마지막 레벨의 노드는 왼쪽부터 빈틈 없이 채워진 트리를 말한다.
트리에서 가장 많이 사용되는 방식이 바로 이 완전 이진트리이다. 추후 다루게 될 우선순위 큐, 힙 등의 자료구조 또한 완전 이진트리의 조건을 갖춰야한다.
완전 이진트리의 특징 중 하나는 노드의 갯수와 트리의 높이와의 관계에서 찾아볼 수 있다.
완전 이진트리의 노드의 개수가 n개 일 때, 그 트리의 높이 h는 log(n)에 비례한다고 할 수 있다.
h = 0일 때 h레벨의 노드의 개수는 총 1개
h = 1일 때 h레벨의 노드의 개수는 총 2개
h = 2일 때 h레벨의 노드의 개수는 총 4개
h = 3일 때 h레벨의 노드의 개수는 총 8개
....
높이가 높아짐에 따라 각 노드 하나당 2개의 자식 노드가 생기므로 각 레벨마다 이전 레벨의 노드의 개수 * 2씩 개수가 증가하는 것을 확인할 수 있다.
이것을 알면 높이가 증가함에 따라 트리의 전체 노드 개수의 범위를 확인할 수 있다.
h의 높이를 가진 트리가 가질 수 있는 전체 노드 개수의 최댓값
h = 0 일 때 2^0 = 1개
h = 1 일 때 2^0 + 2^1 = 3개
h = 2 일 때 2^0 + 2^1 + 2^2 = 7개
h = 3 일 때 2^0 + 2^1 + 2^2 + 2^3 = 15개
....
h = h 일 때 2^0 + 2^1 + .... + 2^h 개
등비수열의 합의 공식을 적용하여 계산하면 전체 노드 개수의 최댓값은 2^h+1 -1개가 된다.
h의 높이를 가진 트리가 가질 수 있는 전체 노드 개수의 최솟값
h = 0 일 때 2^0 = 1개
h = 1 일 때 2^0 + 1 = 2개
h = 2 일 때 2^0 + 2^1 + 1 = 4개
h = 3 일 때 2^0 + 2^1 + 2^2 + 1 = 8개
....
h = h 일 때 2^0 + 2^1 + .... + 2^h-1 + 1 개
마찬가지로 등비수열 합의 공식을 적용하면 전체 노드 개수의 최솟값은 2^h개가 된다.
이걸 부등식으로 정리해보자.
높이가 h인 완전이진트리의 노드의 개수 n은
2^h <= n <= 2^h+1 -1 의 범위안에 있게 된다.
여기서, 높이는 무조건 정수이므로 위의 부등식은
2^h <= n < 2^h+1 로 다시 표현 가능하다.
이제 이 부등식의 모든 값들에 log를 씌워주면,
h <= log(n) < h+1 이 된다.
앞서 말했듯, h는 정수이므로 위 부등식은 "완전이진트리의 높이 h는 전체 노드의 개수 n보다 작은 정수 중 가장 큰 수"로 해석할 수 있다.
다시 말해, 만약 노드가 8개라면 log8 = 3이므로 완전이진트리의 높이는 3이되고,
노드가 11개라면 log8 (3) < log11 < log16(4) 를 만족하므로 여전히 높이가 3이라는 얘기가 된다.
여기서 재밌는 사실을 하나 더 알 수 있다. log n이 정수가 되기 위해선 당연히 2의 거듭제곱수가 되어야할 것이다. 즉, n은 적어도 자기보다 큰 수 중 2의 거듭제곱수보다 큰 숫자가 되어야 완전이진트리의 높이가 1 추가된다는 것이다.
즉, 노드의 개수가 11일 때는 11보다 큰 수 중 2의 거듭제곱 수, 즉 16보다 커지는 순간 트리의 높이가 1 추가된다.
1) 노드 개수 n이 주어질 때, 완전이진트리의 높이를 구하는 함수
# 노드 개수가 주어질 때 완전이진트리의 높이
def complete_binaryTree_height_with_node_number(n):
i = 0
while 2 ** i < n:
i += 1
return i - 1
print(complete_binaryTree_height_with_node_number(37))
2) 완전이진트리의 높이 h가 주어질 때, 해당 트리가 가질 수 있는 총 노드의 최대 개수를 구하는 함수 (재귀함수 이용)
# h 높이의 완전이진트리가 가질 수 있는 노드의 최대 개수
def complete_binaryTree_node_max_number_with_height(h): # 높이 h를 파라미터로
if h == 0: # base case
return 1
return (2 ** h) complete_binaryTree_node_max_number_with_height(h-1)
print(complete_binaryTree_node_max_number_with_height(3))
'그 외 공부 > 자료구조' 카테고리의 다른 글
| 힙(Heap) 자료구조 (0) | 2021.01.30 |
|---|---|
| 이진트리 및 완전이진트리 구현과 순회 (0) | 2021.01.30 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
| 해시테이블의 충돌방지 - Open Addressing (0) | 2021.01.15 |
