힙이란?
힙은 트리 형태로 만들어진 자료구조 중 하나이다.
힙은 트리 중에서도 두 가지 조건을 만족해야 하는데,
첫 번째는 완전이진트리여야 한다는 것
두 번째는 부모 노드의 값이 항상 자신의 자식노드들보다 커야한다는 것이다.
(힙의 예시)
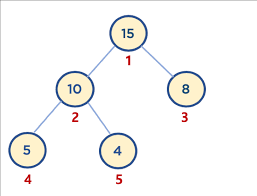
위 트리는 트리의 높이 - 1 까지 모두 빈 노드 없이 차 있으며 마지막 높이의 데이터들 역시 왼쪽부터 오른쪽으로 차례대로 채워져있으므로 완전이진트리의 속성을 만족시킨다고 할 수 있다.
또한, 모든 노드들이 자신의 자식노드들보다 큰 값을 가지기 때문에 힙의 성질 역시 만족시킨다고 할 수 있겠다.
힙 자료구조의 구현
힙 자료구조는 기본적으로 완전이진트리이기 때문에, 특정 노드의 위치를 알면 그 노드의 부모 노드의 위치와 두 자식 노드의 위치를 알 수 있다.
이를 활용하면 각 노드의 값들을 자식 노드들의 값과 비교하는게 가능해지고, 결국 해당 트리가 힙의 성질을 만족하는지 확인할 수 있으며 더 나아가, 힙 성질을 만족시키지 못했던 기존의 완전이진트리들을 힙으로 만들 수도 있다.
그리고 이 알고리즘을 Heapify(힙화)라고 한다.
Heapify는 완전이진트리와 heapify를 하고자하는 인덱스를 인자로 받아 해당 요소를 기준으로 밑 층의 값들이 힙 성질을 만족하는지 확인하고, 만족하지 않는다면 적절히 값의 위치를 바꿔 결국엔 힙으로 만들어주는 역할을 한다.
Heapify 알고리즘의 순서도는 다음과 같다.
1) 인자로 받은 인덱스의 값과 해당 인덱스의 두 자식 노드의 값을 비교해 가장 큰 값을 찾는다.
2) 그렇게 찾은 가장 큰 값이 기존 인자로 받은 인덱스의 값(부모 노드의 값)이 아니라면, 가장 큰 값의 노드와 부모 노드의 위치를 바꾼다.
3) 위치가 변경된 노드(부모 노드에서 자식노드로 내려온 노드)에 대하여 해당 노드의 자식노드들에 대한 heapify를 다시 한 번 수행한다.
* Heapify의 핵심 중 하나는, 노드 간의 위치가 바뀌었을 때, 바뀐 노드에 대해서도 다시 한 번 heapify를 실행해줘야한다는 것이다.
Heapify를 코드로 구현하면 다음과 같다.
def heapify(tree, index):
tree_size = len(tree)
left_child_index = index * 2
right_child_index = index * 2 + 1
# 가장 큰 값의 기본값을 인덱스를 부모노드 인덱스로 설정
largest = index
if left_child_index < tree_size and tree[left_child_index] > tree[largest]:
# 왼쪽 자식의 인덱스가 존재하고 (트리 크기보다 작고), 현재 저장된 가장 큰 값의 값보다 클 때
largest = left_child_index
if right_child_index < tree_size and tree[right_child_index] > tree[largest]:
largest = right_child_index
if largest != index:
# 부모노드가 가장 큰 값이 아닐 때 두 노드를 swap
tree[index], tree[largest] = tree[largest], tree[index]
# 바뀐 노드의 위치에 대하여 다시 한 번 heapify
heapify(tree, largest)
'그 외 공부 > 자료구조' 카테고리의 다른 글
| 단방향 링크드 리스트 뒤집기 - 파이썬 (Python) (1) | 2021.06.13 |
|---|---|
| 이진트리 및 완전이진트리 구현과 순회 (0) | 2021.01.30 |
| 트리 (Tree) 자료구조 (0) | 2021.01.17 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
힙이란?
힙은 트리 형태로 만들어진 자료구조 중 하나이다.
힙은 트리 중에서도 두 가지 조건을 만족해야 하는데,
첫 번째는 완전이진트리여야 한다는 것
두 번째는 부모 노드의 값이 항상 자신의 자식노드들보다 커야한다는 것이다.
(힙의 예시)

위 트리는 트리의 높이 - 1 까지 모두 빈 노드 없이 차 있으며 마지막 높이의 데이터들 역시 왼쪽부터 오른쪽으로 차례대로 채워져있으므로 완전이진트리의 속성을 만족시킨다고 할 수 있다.
또한, 모든 노드들이 자신의 자식노드들보다 큰 값을 가지기 때문에 힙의 성질 역시 만족시킨다고 할 수 있겠다.
힙 자료구조의 구현
힙 자료구조는 기본적으로 완전이진트리이기 때문에, 특정 노드의 위치를 알면 그 노드의 부모 노드의 위치와 두 자식 노드의 위치를 알 수 있다.
이를 활용하면 각 노드의 값들을 자식 노드들의 값과 비교하는게 가능해지고, 결국 해당 트리가 힙의 성질을 만족하는지 확인할 수 있으며 더 나아가, 힙 성질을 만족시키지 못했던 기존의 완전이진트리들을 힙으로 만들 수도 있다.
그리고 이 알고리즘을 Heapify(힙화)라고 한다.
Heapify는 완전이진트리와 heapify를 하고자하는 인덱스를 인자로 받아 해당 요소를 기준으로 밑 층의 값들이 힙 성질을 만족하는지 확인하고, 만족하지 않는다면 적절히 값의 위치를 바꿔 결국엔 힙으로 만들어주는 역할을 한다.
Heapify 알고리즘의 순서도는 다음과 같다.
1) 인자로 받은 인덱스의 값과 해당 인덱스의 두 자식 노드의 값을 비교해 가장 큰 값을 찾는다.
2) 그렇게 찾은 가장 큰 값이 기존 인자로 받은 인덱스의 값(부모 노드의 값)이 아니라면, 가장 큰 값의 노드와 부모 노드의 위치를 바꾼다.
3) 위치가 변경된 노드(부모 노드에서 자식노드로 내려온 노드)에 대하여 해당 노드의 자식노드들에 대한 heapify를 다시 한 번 수행한다.
* Heapify의 핵심 중 하나는, 노드 간의 위치가 바뀌었을 때, 바뀐 노드에 대해서도 다시 한 번 heapify를 실행해줘야한다는 것이다.
Heapify를 코드로 구현하면 다음과 같다.
def heapify(tree, index):
tree_size = len(tree)
left_child_index = index * 2
right_child_index = index * 2 + 1
# 가장 큰 값의 기본값을 인덱스를 부모노드 인덱스로 설정
largest = index
if left_child_index < tree_size and tree[left_child_index] > tree[largest]:
# 왼쪽 자식의 인덱스가 존재하고 (트리 크기보다 작고), 현재 저장된 가장 큰 값의 값보다 클 때
largest = left_child_index
if right_child_index < tree_size and tree[right_child_index] > tree[largest]:
largest = right_child_index
if largest != index:
# 부모노드가 가장 큰 값이 아닐 때 두 노드를 swap
tree[index], tree[largest] = tree[largest], tree[index]
# 바뀐 노드의 위치에 대하여 다시 한 번 heapify
heapify(tree, largest)
'그 외 공부 > 자료구조' 카테고리의 다른 글
| 단방향 링크드 리스트 뒤집기 - 파이썬 (Python) (1) | 2021.06.13 |
|---|---|
| 이진트리 및 완전이진트리 구현과 순회 (0) | 2021.01.30 |
| 트리 (Tree) 자료구조 (0) | 2021.01.17 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
