1) 이진트리
이진트리는 부모 하나 당 최대 2개까지의 자식노드를 가질 수 있는 트리를 말한다.
따라서 이진트리의 각 노드 인스턴스는 자신의 부모 노드에 대한 레퍼런스와 두 자식노드에 대한 레퍼런스를 가지게 된다.
이진트리의 노드 클래스를 구현하면 다음과 같다.
# 이진트리의 노드
class Node:
def __init__(self, data):
# 파라미터로 받은 데이터를 삽입
self.data = data
# None으로 초기값을 지정 후, 노드 생성 후에 지정
self.left_child = None
self.right_child = None
이후, 각 데이터를 담은 노드 클래스를 만들어주고 자식 관계를 설정해주고 나면 노드를 통해 그 노드의 부모노드와 자식노드를 모두 호출할 수 있게 된다.
2) 완전이진트리
완전이진트리는 트리의 높이가 h일 때, h-1층까지는 모든 노드들이 꽉 채워져있고 h번째 층의 값들은 왼쪽부터 차례로 채워져 있는 트리를 말한다.
완전이진트리에 대한 정보는 seongonion.tistory.com/31?category=867075 에서 확인 가능하다.
<구현>
완전이진트리의 노드는 일반적인 이진트리의 노드와 동일하지만, 트리 자체는 파이썬의 리스트를 활용해서 구현할 수 있으며, 이러한 경우에는 굳이 left_child와 right_child를 따로 지정해줄 필요가 없다.
리스트를 통한 완전이진트리의 구현은 리스트에 가장 첫 번째 노드부터 시작해 왼쪽 노드부터 오른쪽 노드까지 차례로 삽입하는 것이다.
예컨데 위와 같은 완전이진트리가 있다면, 이 트리는 리스트로 다음과 같이 구성할 수 있다.
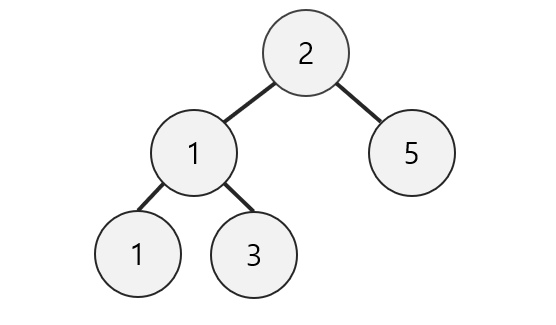
complete_binary_tree = [None, 2, 1, 5, 1, 3]
각 노드의 번호를 리스트의 인덱스로 설정해주기 위해서 가장 첫 번째인 0번 인덱스는 None으로 설정해줌을 알 수 있다.
이러한 파이썬을 통한 구현 방식과 완전이진트리의 특징은 트리의 각 노드의 자식노드와 부모노드의 위치를 알 수 있게 해준다.
이진트리는 각 노드 당 최대 2개까지의 자식노드를 가질 수 있기 때문에, 높이가 1씩 늘어날 때마다 생길 수 있는 최대 원소의 갯수는 직전 층의 최대 원소 개수에 2를 곱한 값이다.
이를 이용하면 우리는 각 노드에 2를 곱하거나 나눔으로써 해당 노드의 자식노드들과 부모노드의 위치를 구할 수 있다.
예를 들어서, 위 트리의 2번째 값 1은 해당 위치에 2를 곱한 4번째 값을 자신의 왼쪽 자식으로 갖는다.
따라서 자연히 자신의 위치에 2를 곱하고 1을 더한 위치에 오른쪽 자식을 갖게 된다.
이를 식으로 정리하면 다음과 같다.
X노드의 왼쪽 자식 노드 == X노드 * 2
X노드의 오른쪽 자식 노드 == X노드 *2 + 1
이를 활용하면 특정 노드의 부모노드를 알 수 있다.
자식 노드의 위치를 구한 것과 반대의 과정을 거치게 되면 X노드의 부모 노드는 X // 2 라는 값이 도출되게 된다.
이를 코드로 구현하면 다음과 같다.
# 부모 노드의 인덱스 위치를 구해주는 함수
def get_parent_index(complete_binary_tree, index):
if index != 1: # 입력된 자식노드가 root노드가 아니라면
return index // 2
else: # 입력된 자식노드가 root노드라면 None을 리턴
return None
# 왼쪽 자식 노드의 위치를 구해주는 함수
def get_left_child_index(complete_binary_tree, index):
# 자식 노드가 있어야할 자리가 트리의 길이를 벗어나지 않는다면
if index * 2 <= len(complete_binary_tree):
return index * 2
else:
return None
def get_right_child_index(complete_binary_tree, index):
if index * 2 + 1 <= len(complete_binary_tree):
return index * 2 + 1
else:
return None
3) 이진트리의 순회
일반적인 링크드 리스트나 배열의 경우 값들이 선형적으로 저장되어있기 때문에, 이들을 순회한다고 하면 자연스레 첫 번째 값부터 마지막번째 값까지 도는 것을 떠올릴 수 있다.
하지만, 트리의 경우 높이에 따른 위 아래가 있을 뿐, 왼쪽과 오른쪽이라는 순서는 존재하지 않기 때문에 배열처럼 선형적인 순회를 하는 것이 불가능하다.
따라서, 이진트리는 트리의 각 데이터들을 순회하는 방식을 다르게 정의해놓았다.
이진트리를 순회하는 방식은 대표적으로 3가지가 있으며, 반복문이 아닌 재귀적 방식을 이용한다.
예컨데, 트리를 순회 하는 traverse 함수를 정의한다고 하면 특정 노드의 왼쪽 부분 트리를 돌고 오른쪽 부분 트리를 도는 동작을 재귀적으로 실행한다는 얘기로,
traverse(node.left_child)
traverse(node.right_child)
와 같이 표현할 수 있겠다.
그리고, 특정 노드를 순회했다는 표시로 해당 노드의 데이터를 출력하는 print(node.data)와 같은 동작을 정의해줄 수 있겠다.
이 세 가지의 동작의 순서를 어떻게 정하냐에 따라서 순회하는 방향이 달라지게 된다.
* 밑에서 설명될 순회 방식은 꼭 한번 읽어보면서 머릿속으로 순서도를 그려보자
1. pre-order 순회 (전위 순회)
pre 는 '~전에' 라는 뜻의 접두사로, 왼쪽과 오른쪽 트리를 순회하기 이전에 노드를 출력하겠다는 의미를 가진다.
이말이 무슨 말이냐면, 위에서 정의한 세 가지 동작을 다음과 같이 진행하겠다는 것이다.
1) 현재 노드를 출력
2) 재귀적으로 왼쪽 부분 트리를 순회
3) 재귀적으로 오른쪽 부분 트리를 순회
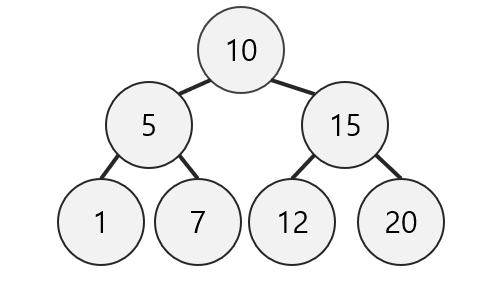
다음의 트리에서 pre-order 방식을 이용하면,
첫 시작노드인 10을 출력 후, 자신의 왼쪽 부분 트리로 이동해 그 곳의 시작값 5를 출력하고, 5의 왼쪽 부분트리로 이동해 그곳의 시작값 1을 출력한다.
1은 더 이상 갈 곳이 없으니 재귀함수가 종료되고 이번엔 5의 오른쪽 부분트리로 이동해 그곳의 시작값 7을 출력한다.
7은 더 이상 이동할 부분트리가 없으므로 재귀함수가 종료되고, 이제는 5 또한 더 이상 순회할 값이 없으니 재귀함수가 종료되고, 10의 왼쪽 부분트리가 모두 순회된 것이다.
이 과정은 다시 10의 오른쪽 부분트리의 시작점인 15에서 또 다시 실행되게 된다.
이 과정을 거치게 되면 트리는
10 -> 5 -> 1 -> 7 -> 15 -> 12 -> 20 순으로 출력되게 된다.
구현도 앞서 말한 로직과 정확히 일치한다.
def pre_order(node):
print(node.data)
if node.left_child != None:
pre_order(node.left_child)
if node.right_child != None:
pre_order(node.right_child)
2. post-order 순회 (후위 순회)
post는 '~후에' 라는 뜻의 접두사로, 말 그대로 왼쪽과 오른쪽 부분트리를 모두 순회한 후 각 노드의 데이터를 출력하겠다는 의미이다.

위와 동일한 트리에서 post-order 방식으로 순회하게 되면
시작 노드인 10의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점인 5는 다시 한 번 자신의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점인 1은 다시 자신의 왼쪽 부분트리를 순회하지만, 값이 없으므로 종료되고 이후에는 자신의 오른쪽 부분트리를 순회한다. 이 역시 존재하지 않으므로 1의 왼쪽, 오른쪽 부분트리의 순회가 끝나고 1이 출력된다.
이 과정은 곧 5의 왼쪽 부분트리에 대한 순회가 끝났음을 의미하며 이번엔 5의 오른쪽 부분트리에 대한 순회가 이루어진다. 오른쪽 부분트리의 시작점은 7은 다시 자신의 왼쪽과 오른쪽 부분트리를 순회하는데, 이 두 값 모두 없으므로 자신의 값인 7을 출력한다.
이렇게 5의 왼쪽 부분트리와 오른쪽 부분트리의 순회가 모두 끝나므로, 5의 값이 출력되게 된다.
이 과정을 모든 노드들에 대하여 반복하게 되면 결국
1 -> 7 -> 5 ->12 -> 20 -> 15 -> 10 의 순서로 출력이 이루어진다.
후위 순회는 전위 순회의 순서 중 출력 부분을 말 그대로 후(post)에 붙여주면 된다.
def post_order(node):
if node.left_child != None:
post_order(node.left_child)
if node.right_child != None:
post_order(node.right_child)
print(node.data)
3. in-order 순회 (중위 순회)
앞선 pre와 post 다음은 in이다. 아마 감이 올 것이다.
중위 순회는 왼쪽 노드를 순회하고 해당 노드의 값을 프린트 한 후에 오른쪽 노드를 순회하는 방식이다.

이번에도 동일한 트리를 돌아보자.
트리의 시작점 10에서 시작해 10의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점 5는 또 다시 자신의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점 1은 또 다시 자신의 왼쪽 부분트리를 순회하는데, 순회할 값이 없으므로 1에 대한 왼쪽 순회 과정이 끝나고 자신의 값 1을 출력한다.
이후, 자신의 오른쪽 부분트리를 순회하는데 이 또한 값이 없으므로 그대로 1에 대한 순회는 종료된다. 이제 5의 왼쪽 부분트리의 순회가 끝났으므로 5의 값이 출력된다.
다음 단계로 5의 오른쪽 부분트리에 대한 순회가 이루어진다. 그리고 오른쪽 부분트리의 시작점인 7에 대한 왼쪽 부분트리의 순회가 다시 이루어지지만, 값이 없으므로 왼쪽 부분트리에 대한 순회가 종료되고 자신의 값 7을 출력한다. 다음으로 7의 오른쪽 부분트리를 순회하지만 이 역시 값이 없으므로 7의 순회는 중료된다. 이제 10의 왼쪽 부분 트리에 대한 순회가 모두 끝난다. 따라서 자신의 값 10이 출력된다.
이 과정을 이후 노드들에도 적용하게 되면 결과적으로
1 -> 5 -> 7 -> 10 -> 12 -> 15 -> 20 의 순서로 출력되게 된다.
중위 순회 또한 출력 실행의 순서만 바꿔주면 곧장 구현 가능하다.
def in_order(node):
if node.left_child != None:
in_order(node.left_child)
print(node.data)
if node.right_child != None:
in_order(node.right_child)'그 외 공부 > 자료구조' 카테고리의 다른 글
| 단방향 링크드 리스트 뒤집기 - 파이썬 (Python) (1) | 2021.06.13 |
|---|---|
| 힙(Heap) 자료구조 (0) | 2021.01.30 |
| 트리 (Tree) 자료구조 (0) | 2021.01.17 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
1) 이진트리
이진트리는 부모 하나 당 최대 2개까지의 자식노드를 가질 수 있는 트리를 말한다.
따라서 이진트리의 각 노드 인스턴스는 자신의 부모 노드에 대한 레퍼런스와 두 자식노드에 대한 레퍼런스를 가지게 된다.
이진트리의 노드 클래스를 구현하면 다음과 같다.
# 이진트리의 노드
class Node:
def __init__(self, data):
# 파라미터로 받은 데이터를 삽입
self.data = data
# None으로 초기값을 지정 후, 노드 생성 후에 지정
self.left_child = None
self.right_child = None
이후, 각 데이터를 담은 노드 클래스를 만들어주고 자식 관계를 설정해주고 나면 노드를 통해 그 노드의 부모노드와 자식노드를 모두 호출할 수 있게 된다.
2) 완전이진트리
완전이진트리는 트리의 높이가 h일 때, h-1층까지는 모든 노드들이 꽉 채워져있고 h번째 층의 값들은 왼쪽부터 차례로 채워져 있는 트리를 말한다.
완전이진트리에 대한 정보는 seongonion.tistory.com/31?category=867075 에서 확인 가능하다.
<구현>
완전이진트리의 노드는 일반적인 이진트리의 노드와 동일하지만, 트리 자체는 파이썬의 리스트를 활용해서 구현할 수 있으며, 이러한 경우에는 굳이 left_child와 right_child를 따로 지정해줄 필요가 없다.
리스트를 통한 완전이진트리의 구현은 리스트에 가장 첫 번째 노드부터 시작해 왼쪽 노드부터 오른쪽 노드까지 차례로 삽입하는 것이다.
예컨데 위와 같은 완전이진트리가 있다면, 이 트리는 리스트로 다음과 같이 구성할 수 있다.

complete_binary_tree = [None, 2, 1, 5, 1, 3]
각 노드의 번호를 리스트의 인덱스로 설정해주기 위해서 가장 첫 번째인 0번 인덱스는 None으로 설정해줌을 알 수 있다.
이러한 파이썬을 통한 구현 방식과 완전이진트리의 특징은 트리의 각 노드의 자식노드와 부모노드의 위치를 알 수 있게 해준다.
이진트리는 각 노드 당 최대 2개까지의 자식노드를 가질 수 있기 때문에, 높이가 1씩 늘어날 때마다 생길 수 있는 최대 원소의 갯수는 직전 층의 최대 원소 개수에 2를 곱한 값이다.
이를 이용하면 우리는 각 노드에 2를 곱하거나 나눔으로써 해당 노드의 자식노드들과 부모노드의 위치를 구할 수 있다.
예를 들어서, 위 트리의 2번째 값 1은 해당 위치에 2를 곱한 4번째 값을 자신의 왼쪽 자식으로 갖는다.
따라서 자연히 자신의 위치에 2를 곱하고 1을 더한 위치에 오른쪽 자식을 갖게 된다.
이를 식으로 정리하면 다음과 같다.
X노드의 왼쪽 자식 노드 == X노드 * 2
X노드의 오른쪽 자식 노드 == X노드 *2 + 1
이를 활용하면 특정 노드의 부모노드를 알 수 있다.
자식 노드의 위치를 구한 것과 반대의 과정을 거치게 되면 X노드의 부모 노드는 X // 2 라는 값이 도출되게 된다.
이를 코드로 구현하면 다음과 같다.
# 부모 노드의 인덱스 위치를 구해주는 함수
def get_parent_index(complete_binary_tree, index):
if index != 1: # 입력된 자식노드가 root노드가 아니라면
return index // 2
else: # 입력된 자식노드가 root노드라면 None을 리턴
return None
# 왼쪽 자식 노드의 위치를 구해주는 함수
def get_left_child_index(complete_binary_tree, index):
# 자식 노드가 있어야할 자리가 트리의 길이를 벗어나지 않는다면
if index * 2 <= len(complete_binary_tree):
return index * 2
else:
return None
def get_right_child_index(complete_binary_tree, index):
if index * 2 + 1 <= len(complete_binary_tree):
return index * 2 + 1
else:
return None
3) 이진트리의 순회
일반적인 링크드 리스트나 배열의 경우 값들이 선형적으로 저장되어있기 때문에, 이들을 순회한다고 하면 자연스레 첫 번째 값부터 마지막번째 값까지 도는 것을 떠올릴 수 있다.
하지만, 트리의 경우 높이에 따른 위 아래가 있을 뿐, 왼쪽과 오른쪽이라는 순서는 존재하지 않기 때문에 배열처럼 선형적인 순회를 하는 것이 불가능하다.
따라서, 이진트리는 트리의 각 데이터들을 순회하는 방식을 다르게 정의해놓았다.
이진트리를 순회하는 방식은 대표적으로 3가지가 있으며, 반복문이 아닌 재귀적 방식을 이용한다.
예컨데, 트리를 순회 하는 traverse 함수를 정의한다고 하면 특정 노드의 왼쪽 부분 트리를 돌고 오른쪽 부분 트리를 도는 동작을 재귀적으로 실행한다는 얘기로,
traverse(node.left_child)
traverse(node.right_child)
와 같이 표현할 수 있겠다.
그리고, 특정 노드를 순회했다는 표시로 해당 노드의 데이터를 출력하는 print(node.data)와 같은 동작을 정의해줄 수 있겠다.
이 세 가지의 동작의 순서를 어떻게 정하냐에 따라서 순회하는 방향이 달라지게 된다.
* 밑에서 설명될 순회 방식은 꼭 한번 읽어보면서 머릿속으로 순서도를 그려보자
1. pre-order 순회 (전위 순회)
pre 는 '~전에' 라는 뜻의 접두사로, 왼쪽과 오른쪽 트리를 순회하기 이전에 노드를 출력하겠다는 의미를 가진다.
이말이 무슨 말이냐면, 위에서 정의한 세 가지 동작을 다음과 같이 진행하겠다는 것이다.
1) 현재 노드를 출력
2) 재귀적으로 왼쪽 부분 트리를 순회
3) 재귀적으로 오른쪽 부분 트리를 순회

다음의 트리에서 pre-order 방식을 이용하면,
첫 시작노드인 10을 출력 후, 자신의 왼쪽 부분 트리로 이동해 그 곳의 시작값 5를 출력하고, 5의 왼쪽 부분트리로 이동해 그곳의 시작값 1을 출력한다.
1은 더 이상 갈 곳이 없으니 재귀함수가 종료되고 이번엔 5의 오른쪽 부분트리로 이동해 그곳의 시작값 7을 출력한다.
7은 더 이상 이동할 부분트리가 없으므로 재귀함수가 종료되고, 이제는 5 또한 더 이상 순회할 값이 없으니 재귀함수가 종료되고, 10의 왼쪽 부분트리가 모두 순회된 것이다.
이 과정은 다시 10의 오른쪽 부분트리의 시작점인 15에서 또 다시 실행되게 된다.
이 과정을 거치게 되면 트리는
10 -> 5 -> 1 -> 7 -> 15 -> 12 -> 20 순으로 출력되게 된다.
구현도 앞서 말한 로직과 정확히 일치한다.
def pre_order(node):
print(node.data)
if node.left_child != None:
pre_order(node.left_child)
if node.right_child != None:
pre_order(node.right_child)
2. post-order 순회 (후위 순회)
post는 '~후에' 라는 뜻의 접두사로, 말 그대로 왼쪽과 오른쪽 부분트리를 모두 순회한 후 각 노드의 데이터를 출력하겠다는 의미이다.

위와 동일한 트리에서 post-order 방식으로 순회하게 되면
시작 노드인 10의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점인 5는 다시 한 번 자신의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점인 1은 다시 자신의 왼쪽 부분트리를 순회하지만, 값이 없으므로 종료되고 이후에는 자신의 오른쪽 부분트리를 순회한다. 이 역시 존재하지 않으므로 1의 왼쪽, 오른쪽 부분트리의 순회가 끝나고 1이 출력된다.
이 과정은 곧 5의 왼쪽 부분트리에 대한 순회가 끝났음을 의미하며 이번엔 5의 오른쪽 부분트리에 대한 순회가 이루어진다. 오른쪽 부분트리의 시작점은 7은 다시 자신의 왼쪽과 오른쪽 부분트리를 순회하는데, 이 두 값 모두 없으므로 자신의 값인 7을 출력한다.
이렇게 5의 왼쪽 부분트리와 오른쪽 부분트리의 순회가 모두 끝나므로, 5의 값이 출력되게 된다.
이 과정을 모든 노드들에 대하여 반복하게 되면 결국
1 -> 7 -> 5 ->12 -> 20 -> 15 -> 10 의 순서로 출력이 이루어진다.
후위 순회는 전위 순회의 순서 중 출력 부분을 말 그대로 후(post)에 붙여주면 된다.
def post_order(node):
if node.left_child != None:
post_order(node.left_child)
if node.right_child != None:
post_order(node.right_child)
print(node.data)
3. in-order 순회 (중위 순회)
앞선 pre와 post 다음은 in이다. 아마 감이 올 것이다.
중위 순회는 왼쪽 노드를 순회하고 해당 노드의 값을 프린트 한 후에 오른쪽 노드를 순회하는 방식이다.

이번에도 동일한 트리를 돌아보자.
트리의 시작점 10에서 시작해 10의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점 5는 또 다시 자신의 왼쪽 부분트리를 순회한다. 왼쪽 부분트리의 시작점 1은 또 다시 자신의 왼쪽 부분트리를 순회하는데, 순회할 값이 없으므로 1에 대한 왼쪽 순회 과정이 끝나고 자신의 값 1을 출력한다.
이후, 자신의 오른쪽 부분트리를 순회하는데 이 또한 값이 없으므로 그대로 1에 대한 순회는 종료된다. 이제 5의 왼쪽 부분트리의 순회가 끝났으므로 5의 값이 출력된다.
다음 단계로 5의 오른쪽 부분트리에 대한 순회가 이루어진다. 그리고 오른쪽 부분트리의 시작점인 7에 대한 왼쪽 부분트리의 순회가 다시 이루어지지만, 값이 없으므로 왼쪽 부분트리에 대한 순회가 종료되고 자신의 값 7을 출력한다. 다음으로 7의 오른쪽 부분트리를 순회하지만 이 역시 값이 없으므로 7의 순회는 중료된다. 이제 10의 왼쪽 부분 트리에 대한 순회가 모두 끝난다. 따라서 자신의 값 10이 출력된다.
이 과정을 이후 노드들에도 적용하게 되면 결과적으로
1 -> 5 -> 7 -> 10 -> 12 -> 15 -> 20 의 순서로 출력되게 된다.
중위 순회 또한 출력 실행의 순서만 바꿔주면 곧장 구현 가능하다.
def in_order(node):
if node.left_child != None:
in_order(node.left_child)
print(node.data)
if node.right_child != None:
in_order(node.right_child)'그 외 공부 > 자료구조' 카테고리의 다른 글
| 단방향 링크드 리스트 뒤집기 - 파이썬 (Python) (1) | 2021.06.13 |
|---|---|
| 힙(Heap) 자료구조 (0) | 2021.01.30 |
| 트리 (Tree) 자료구조 (0) | 2021.01.17 |
| 스택 (Stack) 자료구조 (0) | 2021.01.15 |
| 큐 (Queue) 자료구조 (0) | 2021.01.15 |
